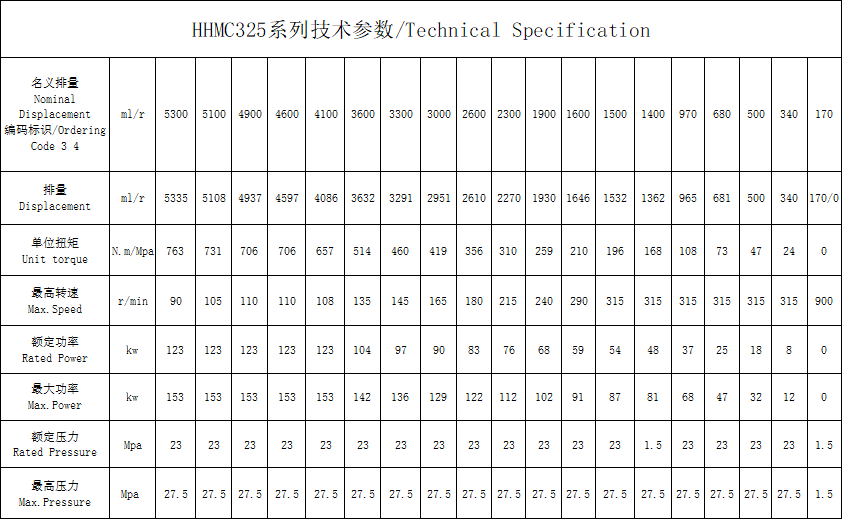
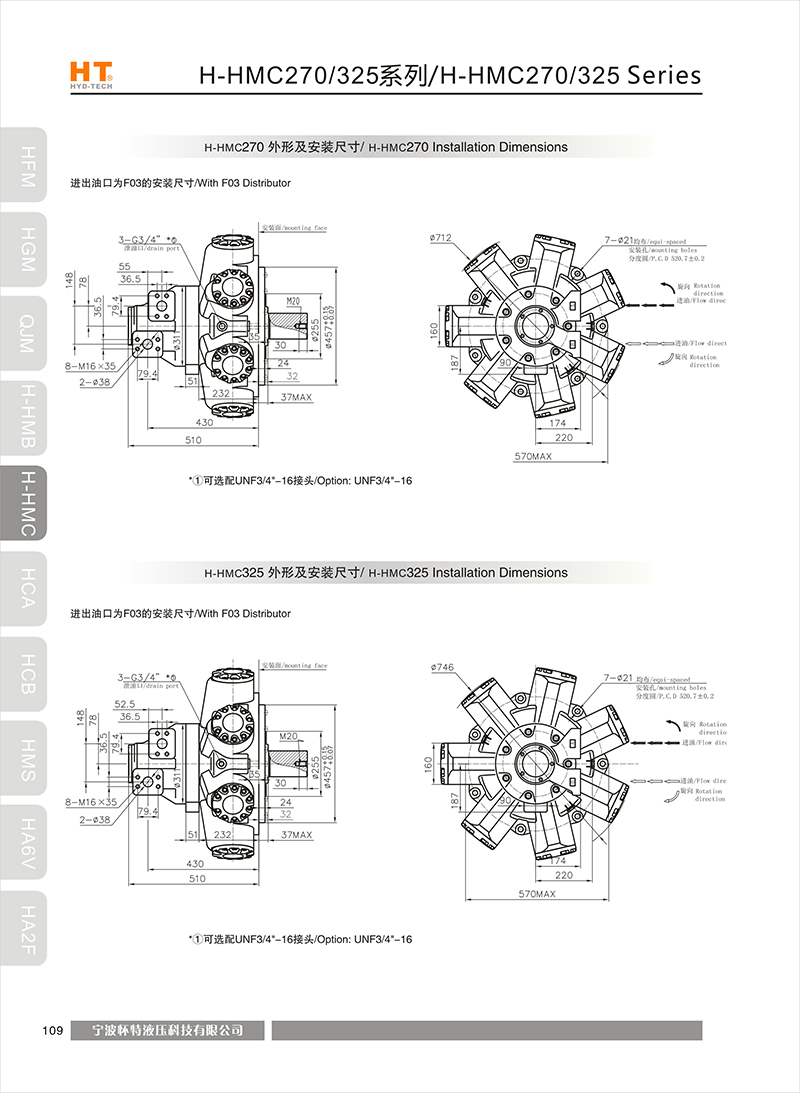
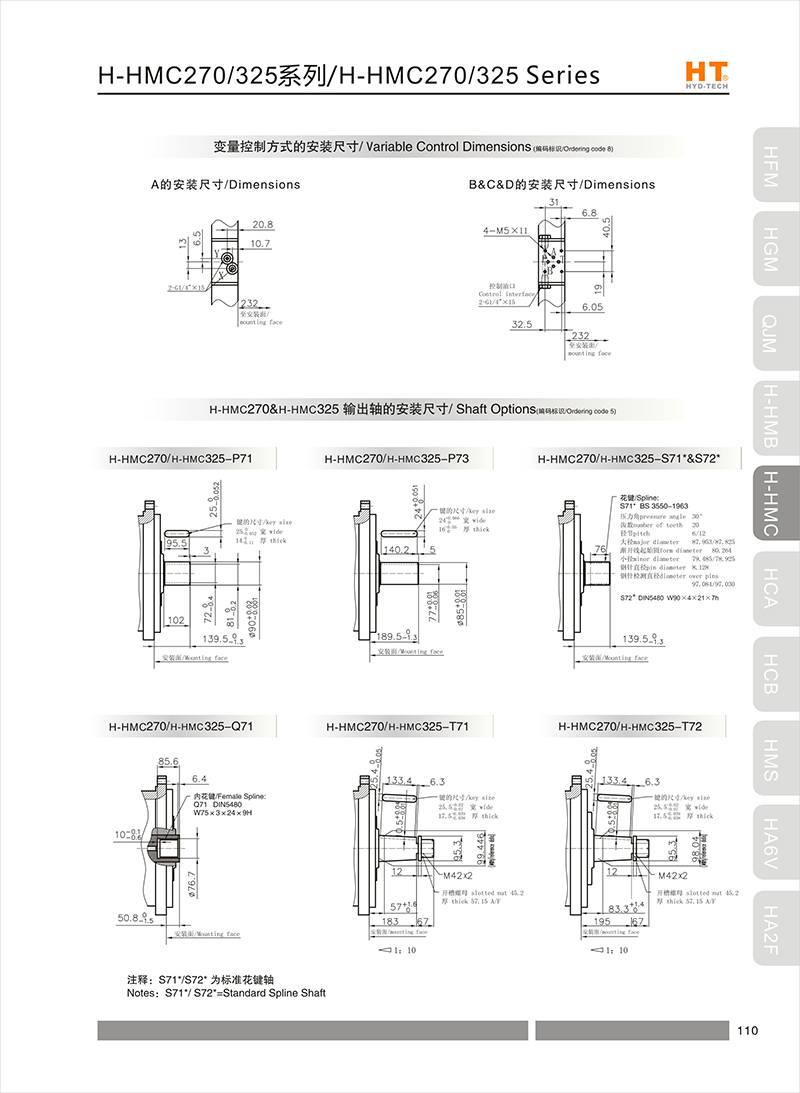
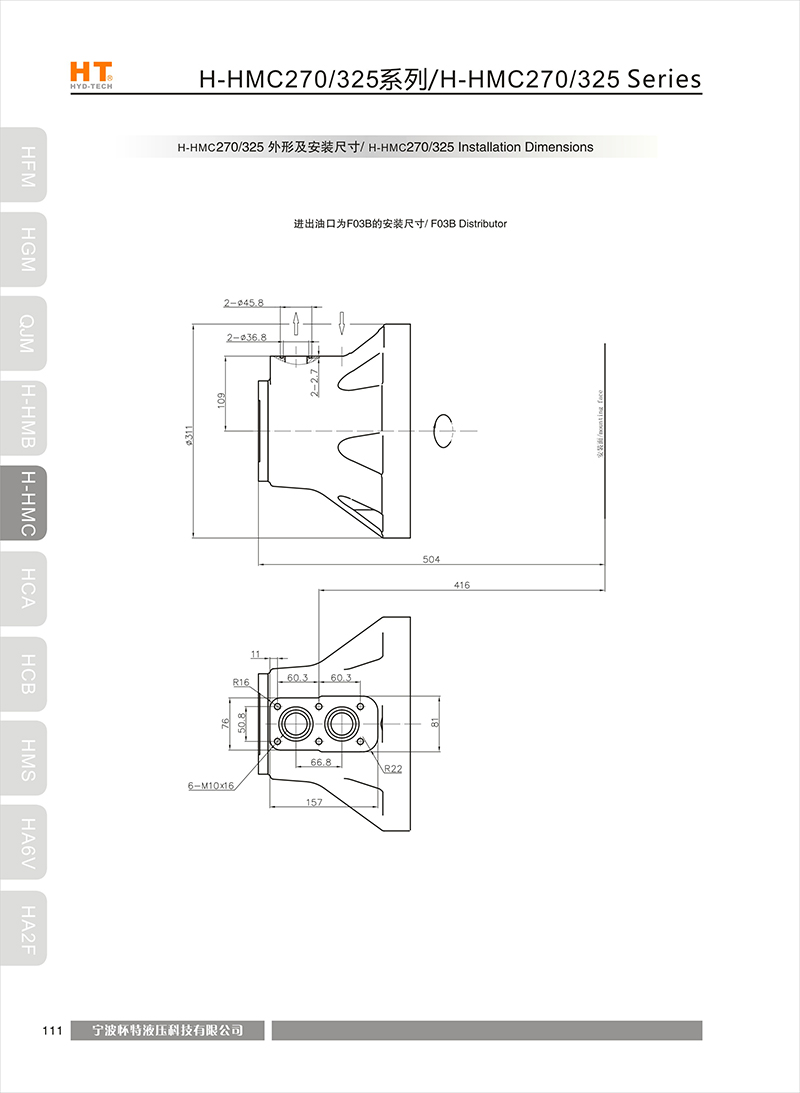
Network optimization information:
When a high-rise building is on fire, the most urgent and important problem is to rescue the residents on the high-rise building from the building on fire as soon as possible. At this time, if there is a long soft belt that people can step on and slide to the ground, it is undoubtedly a good solution. However, what kind of curve can this long soft belt turn into so that people can escape from the fire as quickly as possible? That is the question of the fastest route.
In 1630, the Italian scientist Galileo put forward this question and abstracted it into one of the basic problems of analytical science.
"If there is no friction, the sliding distance between two straight lines is the shortest when a particle moves from a given point A to another point B that is not perpendicular to it under the action of gravity." Obviously, the straight line cannot be the fastest deceleration line. Galileo believes that this curve is an arc, but this is also the wrong answer.
In 1696, the Swiss mathematician John Bernoulli took a challenging tone, Cycloidal hydraulic motor BMT Again, I asked mathematicians all over Europe for the answer to the steepest descent line. The next year, many mathematicians, including Newton, Leibniz, Lobida, John Bernoulli and his brother Jacob Bernoulli, found the correct answer. The difficulty of this problem lies in the difference between the general known function of the minimum value and the minimum value function of the minimum value function, Special cycloidal motor for hydraulic winch It requires an unknown function (curve) to meet the given conditions. The correct answer is a cycloid connecting the depressions on two points. Orla, a mathematician who was a student of John Burnully, also began to publish relevant papers in 1726. He first proposed a universal solution to such problems in 1744, which led to the emergence of the new branch of mathematics, variational method.




![]()

